Section 33–2 Polarization of scattered light

(Rayleigh scattering / Random polarizations / Lateral scattering)

 

In this section, Feynman briefly discusses Rayleigh scattering, random polarizations, and lateral scattering. In the Audio Recordings* [14 min: 05 sec], Feynman says something like: “If there is a beam of light like the Sun shining on the air, it will have an electric field say this way or in this way, it will change if it is unpolarized. If we stand down over here, we see that when I am doing the time that it is polarized in this direction, the wave will be generated this way (scattered wave) by the motion of charge in the air. On the other hand, when the light is polarised this way during the time that it is doing that during the unpolarised (averaging in space) because the current is in the line of sight, so there is no field generated in the eye, when it is this way, all the field would be generated in the eye is polarised up and down.” This section is heavily edited, but there could be some diagrams to explain the polarization of scattered light. It could also be titled “Polarization by scattering of light” because the next section is about “Polarization by absorption.”

 

*The Feynman Lectures Audio Collection: https://www.feynmanlectures.caltech.edu/flptapes.html

 

1. Rayleigh Scattering:

“The first example of the polarization effect that we have already discussed is the scattering of light. Consider a beam of light, for example from the sun, shining on the air. The electric field will produce oscillations of charges in the air, and motion of these charges will radiate light with its maximum intensity in a plane normal to the direction of vibration of the charges (Feynman et al., 1963, p. 33-3).”

 

The term scattering refers to Rayleigh scattering, i.e., the absorption of light by a particle and the emission of light due to the particle’s oscillation. In other words, the electric field of the incoming light oscillates the electrons, and the oscillated electrons will emit scattered light (or secondary waves) in different directions. However, some may not be able to visualize the plane, normal to the direction of vibration of the charges, that has maximum intensity. Specifically, the radiation pattern due to the scattering of a single molecule has a doughnut (or donut) shape (see Fig. 1) and the intensity is zero along the direction of the oscillation of the charge. Strictly speaking, the intensity would not be zero because of multiple scattering and the air molecules are randomly oriented.

Fig. 1

 

We can deduce the radiation pattern of an oscillating charge to be doughnut-shaped using the third term of the Feynman-Heaviside expression of accelerated charge (equation 28.3). This helps to explain why Feynman says: “motion of these charges will radiate light with its maximum intensity in a plane normal to the direction of vibration of the charges.” To be precise, maximum intensity occurs at a horizontal plane if the charge is oscillating vertically. This radiation pattern is an idealization because the oscillation of the charge is not always along the same axis. In the real world, we may imagine the radiation pattern to be a rotatable doughnut about the direction of propagation of light (z-axis) and it is dependent on the linear polarization of light in the x-axis or y-axis.

 

2. Random polarizations:

The beam from the sun is unpolarized, so the direction of polarization changes constantly, and the direction of vibration of the charges in the air changes constantly (Feynman et al., 1963, p. 33-3).

 

Instead of saying “the beam from the Sun is unpolarized,” we may clarify that the wave packets emitted by the Sun are randomly polarized. Firstly, the term wave packet means a short oscillatory directional pulse that is emitted within a duration on the order of 10^-8 s to 10^-9 s. This corresponds to a state of atomic excitation (or a short-lived resonance phenomenon) whereby the excited atom spontaneously relaxes back to a lower state and loses the excitation energy. On the other hand, the Sun consists of a very large number of randomly oriented atomic emitters and the wave packets from the Sun are randomly polarized. Thus, the direction of polarization changes randomly and the direction of vibration of the charges in the air changes randomly (instead of changing constantly).

 

Perhaps Feynman could have mentioned there was a crisis in optics over the challenge to develop a general formula of randomly and partially polarized light. In 1852, Sir George Gabriel Stokes, Rayleigh’s optics teacher, proposed that any polarization state can be completely described by four measurable quantities or parameters. The four Stokes parameters are not dependent on a coordinate system, but they can be easily calculated or measured. For example, we can investigate the pulsar in the Crab Nebula using Stokes parameters and measuring its optical and radio-frequency radiation. (Feynman discusses the radiation emitted by the Crab Nebula in the next chapter.) However, some may argue whether linearly and circularly polarized light are special cases of elliptically polarized light from the perspective of Stokes parameters.

 

3. Lateral scattering:

“If we consider light scattered at 90^o, the vibration of the charged particles radiates to the observer only when the vibration is perpendicular to the observer’s line of sight, and then light will be polarized along the direction of vibration (Feynman et al., 1963, p. 33-3).”

 

Fig. 2 (Source: https://byjus.com/physics/polarisation-by-scattering/)

It may not be clear why “Feynman” says the light will be polarized along the direction of vibration if it is scattered at 90^o and the vibration is perpendicular to the observer’s line of sight. This could be illustrated using a diagram (see Fig. 2): Firstly, the scattered light rays that are parallel to the incoming light are completely unpolarised. Secondly, the light rays scattered at 90^o are completely polarized because there is no polarized light that oscillates in the direction of the incoming light. (Based on the definition of polarized light, the electric field of incoming light and scattered light “cannot oscillate longitudinally” in the direction of propagation of light.) Thirdly, the scattered light rays in all other directions (between 0^o and 90^o) are partially polarized. To be precise, the light scattered at 90^o is maximally polarized (instead of completely polarized) because of multiple and random scattering.

 

Fig. 3

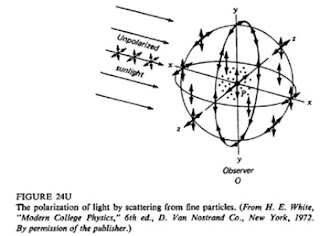
The “light scattered at 90^o” (lateral scattering) can occur at an infinite number of possible angles (Fig. 3). In general, the lateral scattering of light by a single molecule could be elaborated from the perspective of horizontally (x-direction) and vertically (y-direction) polarized light (Fig. 4). If the incoming light is moving in the z-direction and horizontally polarized, the light scattered in the y-direction (upward or downward) should remain as horizontally polarized. If the incoming light is moving in the z-direction and vertically polarized, the light scattered in the x-direction (toward or away from the observer) should remain vertically polarized. Although we can assume polarized light to have no longitudinal component, but this assumption is violated in a glass fiber (Junge et al., 2013).

 

Fig. 4

Review Questions:

1. How would you explain the oscillation of charges in the air radiates light with its maximum intensity in a plane normal to the direction of vibration of the charges?

2. Does the direction of vibration of the charges in the air change constantly (or randomly?) if the sunlight is unpolarized?

3. How would you explain the light is maximally polarized if it is scattered at 90^o?

 

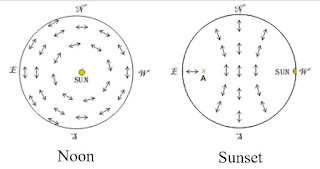
The moral of the lesson: Light rays are horizontally polarized along the entire horizon when the sun is high up in the sky at noon, but they are maximally polarized along the meridian that passes through the zenith during sunset (See Fig. 5).

 

Fig. 5

Note: In Chapter 36, Feynman elaborates: “The bee can tell, because the bee is quite sensitive to the polarization of light, and the scattered light of the sky is polarized.” In 1949, Karl von Frisch established that bees, through their perception of polarized light, are able to remember polarization patterns presented by the sky at different times of the day when the Sun is not visible. Karl von Frisch is awarded the Nobel Prize in Physiology or Medicine 1973 for explaining the waggle dance used by bees to communicate the location of food sources.

 

References:

1. Feynman, R. P. (1985). QED: The strange theory of light and matter. Princeton: Princeton University Press.

2. Feynman, R. P., Leighton, R. B., & Sands, M. (1963). The Feynman Lectures on Physics, Vol I: Mainly mechanics, radiation, and heat. Reading, MA: Addison-Wesley.

3. Junge, C., O’shea, D., Volz, J., & Rauschenbeutel, A. (2013). Strong coupling between single atoms and nontransversal photons. Physical review letters, 110(21), 213604.