Section 38–2 Measurement of position and momentum

(Single slit / Diffraction grating / Uncertainty relation)

 

In this section, Feynman discusses the uncertainty of complementary variables involving a slit and diffraction grating, as well as the uncertainty relation in wave theory. A more fitting title for this section might be “Inherent Uncertainty of Position and Momentum.” It emphasizes that while measurement can increase uncertainty, the uncertainty itself is intrinsic to the system rather than solely a result of measurement (as implied by the title, “Measurement of Position and Momentum”).

 

1. Single slit:

“How does the pattern become spread? To say it is spread means that there is some chance for the particle to be moving up or down, that is, to have a component of momentum up or down. We say chance and particle because we can detect this diffraction pattern with a particle counter, and when the counter receives the particle, say at C in Fig. 38–2, it receives the entire particle, so that, in a classical sense, the particle has a vertical momentum, in order to get from the slit up to C (Feynman et al., 1963, p. 38–2).”

 

Feynman explains diffraction through a single slit using a particle-based perspective. While this explanation aligns with quantum mechanics’ probabilistic nature, it reflects Feynman’s preference for a particle-centric view. In wave theory, light can be represented as wave packets, which are superpositions of waves with slightly different wavelengths. The wave packets may provide a better understanding of diffraction, where the single slit acts as a device that spreads the wave’s wavelength components across a range of angles. The relationship between the slit width and the diffraction pattern can be understood via the uncertainty principle: narrowing the slit increases uncertainty in the momentum of wave packets, resulting in a broader angular spread, and vice versa.

 

The spreading of wave packets by the slit can be interpreted as an environmental interaction, but it is equivalent to a measurement. As light passes through a slit, it becomes localized, effectively corresponding to a position measurement. However, this localization in position introduces an uncertainty in the vertical wave number k_y​, which is directly related to the vertical momentum p_y​ (= ℏk_y​). Based on the wave theory, when the wave packet is highly localized, the momentum uncertainty (Δp_y) is large, causing greater spreading. In this framework, the spreading of the wave packet is not a result of the particle "moving up or down" in the classical sense, but rather an inherent property of wave-like behavior arising from the superposition of wave components.

 

“Sometimes people say quantum mechanics is all wrong. When the particle arrived from the left, its vertical momentum was zero. And now that it has gone through the slit, its position is known. Both position and momentum seem to be known with arbitrary accuracy (Feynman et al., 1963, p. 38–3).”

 

It is worth mentioning that Einstein did not say quantum mechanics was all wrong, but critiqued its completeness. His concern was whether quantum mechanics provides a complete description of reality or merely reflects statistical ignorance of some deeper, hidden reality. Instead of assuming a perfect correlation between a wave packet’s position and momentum, it is crucial to recognize the predictive limitations of quantum mechanics. Once a particle or wave packet interacts with the slit, its momentum is irreversibly disturbed, i.e., the act of measurement (position localization) fundamentally alters the system, increasing momentum uncertainty. However, questions about the nature of quantum correlations and their possible connections to deeper underlying mechanisms continue to drive theoretical and experimental investigations.

 

2. Diffraction grating:

“Suppose we have a grating with a large number of lines (Fig. 38–3), and send a beam of particles at the grating…… That is, the waves which form the diffraction pattern are waves which come from different parts of the grating. The first ones that arrive come from the bottom end of the grating, from the beginning of the wave train, and the rest of them come from later parts of the wave train, coming from different parts of the grating, until the last one finally arrives, and that involves a point in the wave train a distance L behind the first point (Feynman et al., 1963, p. 38–3).”

 

It is remarkable that Feynman used Rayleigh’s criterion of resolution to derive an uncertainty relation, but this criterion is not based on a fundamental physical principle—it is a guideline or convention for resolving two overlapping waves. The key factor in determining the diffraction pattern produced by a grating is the spread of wavelengths within the wave trains. The length of a wave train is crucial because it is directly related to its wavelength spread (Δλ). A longer wave train has a narrower spread of wavelengths, leading to sharper and distinct diffraction peaks, and vice versa. The term wave train is appropriate here because it conveys the idea of a longer wave, as compared to the shorter localized wave packet, which is more apt for modeling particles passing through a single slit.

 

The sharpness of diffraction peaks is not fundamentally limited by the grating itself but rather by the spectral composition (distribution of wavelengths and relative strengths) of the wave train.  If the wavelength spread (Δλ) of the wave train exceeds the grating’s resolving capability, the diffraction pattern will remain blurred, regardless of the number of lines on the grating or width of the slits. Interestingly, the distance L, corresponding to the wave train’s coherence length, can also be interpreted as the minimum length required for using the entire grating effectively. More important, the grating functions like a Fourier transform, decomposing the wave train into its constituent wavelengths. This is analogous to how the human ear—specifically, the cochlea, a fluid-filled spiral structure—distinguishes sounds of different frequencies (See below).

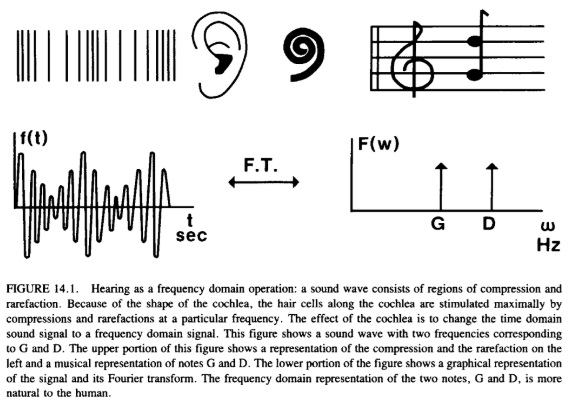(Source: Parker, 2018)

 

3. Uncertainty relation:

“Now this property of waves, that the length of the wave train times the uncertainty of the wave number associated with it is at least 2π, is a property that is known to everyone who studies them. It has nothing to do with quantum mechanics. It is simply that if we have a finite train, we cannot count the waves in it very precisely (Feynman et al., 1963, p. 38–4).”

 

Feynman’s remark underscores a fundamental fact: a finite wave train does not have a precisely defined wavelength (or wave number). More generally, the product of uncertainties in wave number (Δk) and position (Δx, the length of a wave packet or wave train) can be normalized to a constant such as 2π or 1 for simplicity (see below), depending on the chosen units. This reflects the nature of waves rather than being tied to any specific measurement process. The spectral composition of a wave train depends on its length: a long wave train consists of a narrow spread of wavelengths, akin to playing a single note on a flute for an extended time—an almost pure tone. Conversely, a short wave train has a broad range of frequencies, similar to pressing all the keys on a piano simultaneously, thereby produces a short burst of sound. In short, the length of the wave train tells us about how “pure” or “mixed” the wave is (in terms of its wavelength).

Source: Wave Equation, Wave Packet Solution

The uncertainty relation in wave theory is closely related to Fourier series, where any wave can be represented as a sum of sinusoidal components. Though Feynman does not explicitly specify Fourier transforms, his discussion aligns with Fourier’s principles. Essentially, a shorter wave train needs more wave components of differing wavelengths to form its sharp edges and transient nature, whereas a longer wave train is dominated by a narrower set of frequencies, resulting in a smoother, more uniform waveform. This relation underscores the fundamental trade-off between localization in space and precision in wavelength, mirroring the uncertainty principle in quantum mechanics. This insight, deeply rooted in Fourier analysis, provides a mathematical foundation for understanding the intrinsic limits of measurement in both classical wave theory and quantum mechanics.

 

Note: The section title “Measurement of position and momentum” could be misleading, as the uncertainty relation applies universally to wave phenomena, not just quantum measurement. In a paper on the quantum postulate, Bohr (1928) expressed this clearly: “[r]igorously speaking, a limited wave-field can only be obtained by the superposition of a manifold of elementary waves corresponding to all values of ν and σ_x, σ_y, σ_z. But the order of magnitude of the mean difference between these values for two elementary waves in the group is given in the most favourable case by the condition Δt Δν = Δx Δσ_x = Δy Δσ_y = Δz Δσ_z = 1, where Δt, Δx, Δy, Δz denote the extension of the wave-field in time and in the directions of space corresponding to the co-ordinate axes. These relations — well known from the theory of optical instruments, especially from Rayleigh's investigation of the resolving power of spectral apparatus — express the condition that the wave-trains extinguish each other by interference at the space-time boundary of the wave-field.”

 

Review Questions:

1. How would you explain the spreading of a particle (or wave packet) through a slit?

2. Is it legitimate to derive an uncertainty relation using the Rayleigh’s criterion of resolution?

3. How would you explain inherent uncertainties using the Fourier Transform?

 

The moral of the lesson: The uncertainty of complementary variables in quantum mechanics—whether in a slit or diffraction grating—can be changed by environmental conditions or measurement, however, the uncertainty relation is already known as an inherent property of waves before the quantum revolution.

 

References:

1. Bohr, N. (1928). The Quantum Postulate and the Recent Development of Atomic Theory. Nature, 121, 580-590.

2. Feynman, R. P., Leighton, R. B., & Sands, M. (1963). The Feynman Lectures on Physics, Vol I: Mainly mechanics, radiation, and heat. Reading, MA: Addison-Wesley.

3. Parker, J. A. (2018). Image reconstruction in radiology. Boca Raton, FL: CRC press.